Empirical Benchmark Evidence

Demonstrating that catastrophic forgetting behaviors are observable, reproducible, and reversible across multiple base models under consistent evaluation conditions.

Evaluation Methodology

All benchmarks were executed using the same evaluation harness, task definitions, and zero-shot configuration across all training phases. This consistency ensures that observed performance changes reflect genuine model state transitions rather than evaluation artifacts.

The evaluation framework assessed models across three distinct phases:

Key benchmarks evaluated include ARC Challenge (reasoning), GSM8K with Chain-of-Thought (mathematical reasoning), HellaSwag (common sense), and Winogrande (logical inference). These benchmarks were selected to capture both domain-specific and general capabilities.

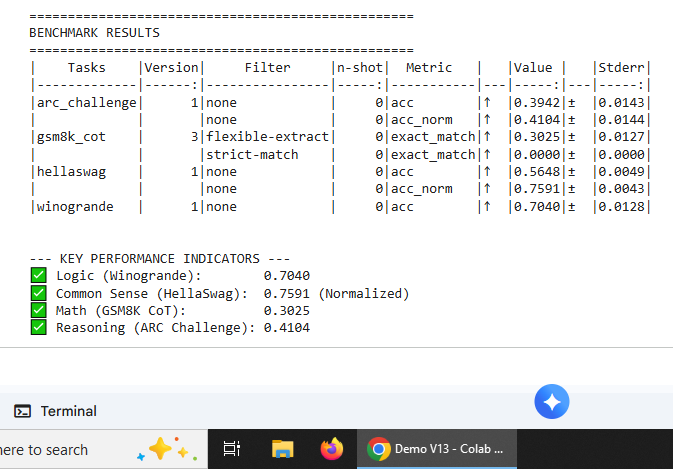
Nous-Hermes-llama-2-7b

First validation model demonstrating selective degradation and recovery patterns

Baseline Phase 1

Initial model state prior to domain-specific training. Establishes baseline performance across all evaluated benchmarks.

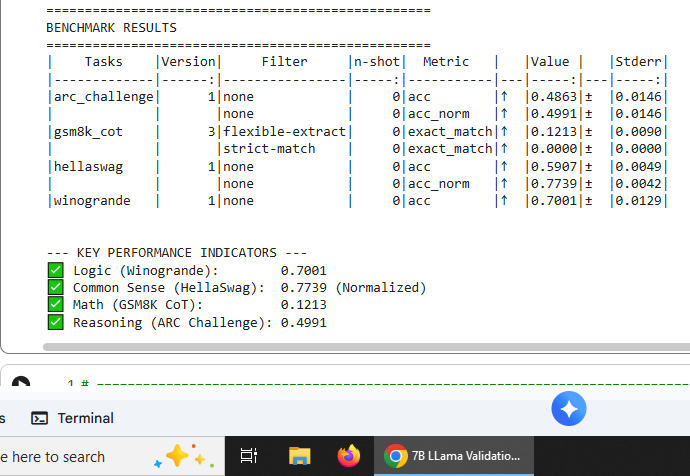
Nous-Hermes Baseline Benchmarks
Math Training Phase 2

Post mathematics-focused fine-tuning. Demonstrates selective degradation in ARC Challenge while maintaining or improving performance in other domains.

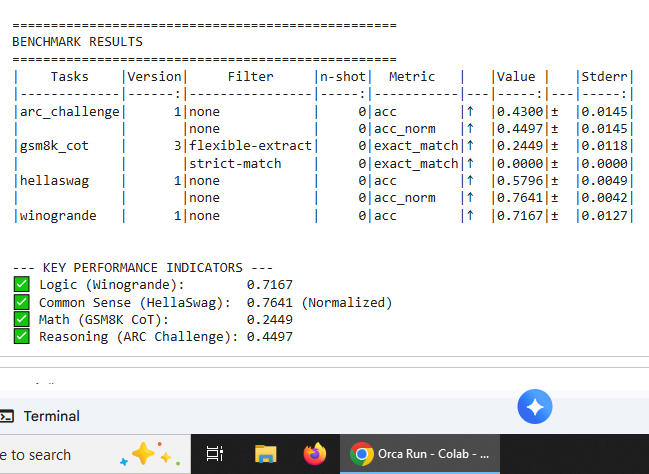
Nous-Hermes Math Training Benchmarks
ARC Recovery Phase 3

Recovery phase demonstrating restoration of ARC performance without reintroduction of original training data, supporting inference misrouting hypothesis.

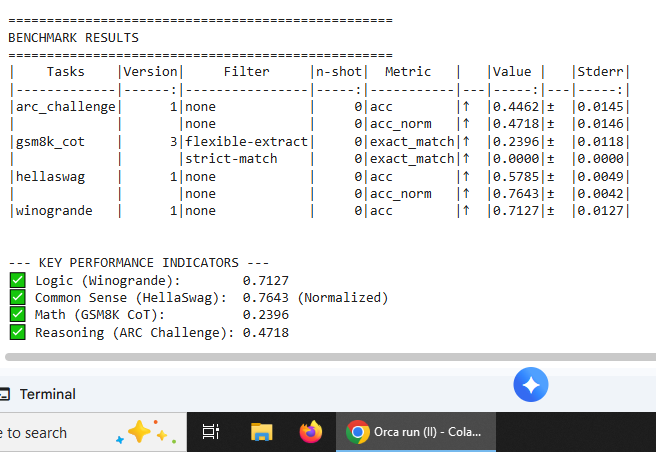
Nous-Hermes ARC Recovery Benchmarks

Llama-2-7b-chat-hf

Independent validation across a second model family confirming reproducibility of observed patterns

Baseline Phase 1

Baseline evaluation establishing initial capability profile. Provides comparison point for subsequent training phases.

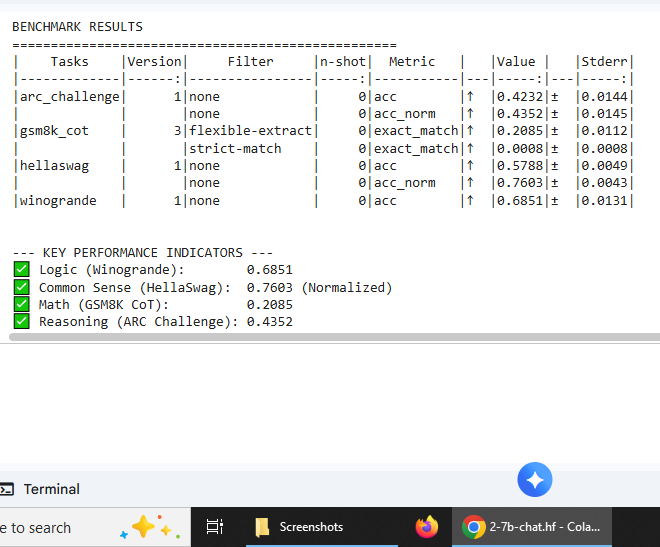
Llama-2 Baseline Benchmarks
Math Training Phase 2

Mathematics-focused training phase exhibiting consistent degradation patterns with Nous-Hermes model, confirming cross-model reproducibility.

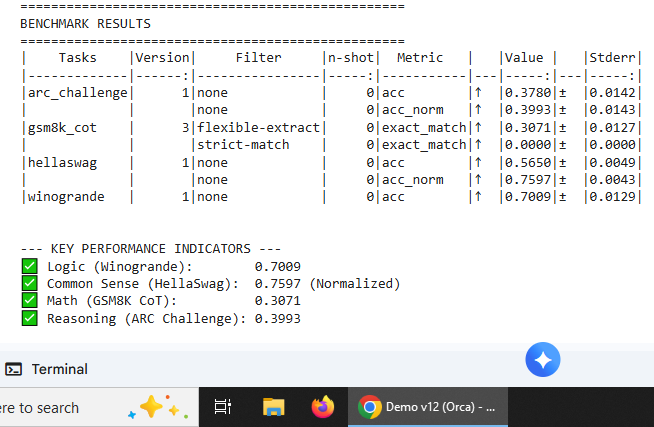
Llama-2 Math Training Benchmarks
ARC Recovery Phase 3

Recovery phase validating that observed degradation is reversible across different model architectures and training histories.

Llama-2 ARC Recovery Benchmarks

Key Empirical Observations

Selective Degradation: Performance regressions are domain-localized rather than uniform. ARC Challenge scores decline following math-focused training while other benchmarks remain stable or improve.
Cross-Model Consistency: Both Nous-Hermes and Llama-2 models exhibit similar degradation and recovery patterns, suggesting systematic rather than model-specific behavior.
Reversibility Without Retraining: ARC performance recovery occurs without reintroduction of original training data, supporting the inference misrouting hypothesis over irreversible knowledge loss.
Maintained Mathematical Gains: Recovery of ARC performance does not sacrifice mathematical capability improvements, indicating successful multi-domain integration.
Evaluation Consistency: All measurements conducted under identical evaluation protocols, eliminating confounding variables from prompt or configuration changes.
← Back to Home